Today I’m finally going to finish up the series I started on image processing. The goal of this series is to dispel any myths that algorithms that work on images make things up or do strange, arcane magic. The data is there in the images already, and algorithms that work on them simply make things more visible to a human.
My idea for this originally started when people claimed that zooming in on an image using an iPhone was somehow changing it. The claim (politically motivated) was that it changed the semantic content of the image by zooming in or out. So today I’ll wrap up this series by going over how you zoom an image (or make it larger / smaller). Note this post will be a bit more technical than the last one as I am including code to demonstrate what I am doing.
Semantic content of an image refers to the meaning or information that the image conveys, such as objects, scenes, actions, attributes, etc. For example, if you take a picture of a cat sitting on a table in your kitchen, then the semantic content would be each of the objects that are in that image (cat, table, kitchen).
Images are resized for you automatically all the time, and you are never aware of it mostly. Your web browser will scale an image so that it fits on your screen. Mobile devices scale images such that you can fit them on the device display. You may even have “pinch to zoom” in on an image so you can see things more clearly. So ask yourself, when you have zoomed in on an image, do new objects suddenly appear in it? Does an elephant suddenly appear when you zoom in or out of a picture of your children? You would have noticed this by now should it happen.
Yes, any time you resize an image you do technically change it, as you have to map pixels from the original to the new size. However, no resizing operation changes the semantic content of the image. People have been mapping things and rescaling them long before computers have existed. Architects, draftsmen, cartographers, and others were transforming and resizing things before electricity was discovered. Just because a computer does it does not mean that suddenly objects get inserted into the image or that the meaning of the image gets changed.
I’ll be using OpenCV 4 and Python 3. For those unaware, OpenCV is an open source computer vision library that has been around for a long time and is used in thousands of projects. The algorithms in it are some of the best around and have been vetted by experts in the field. The example image I will be using is a public domain image of a fish as can be seen below.
To play along at home, I have the source code for this blog post at https://github.com/briangmaddox/blog_opencv_resizing_example
The first thing we do with our sample image is to load it in using OpenCV, print the dimensions, and then display it.
# Load in our input image
input_image = cv2.imread("1330-sole-fish.jpg")
# Get the dimensions of the original image
height, width, channels = input_image.shape
# Print out the dimensions
print(f"Image Width: {width} Height: {height}")
# Display the original image to the user
cv2.imshow("Original Image", input_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
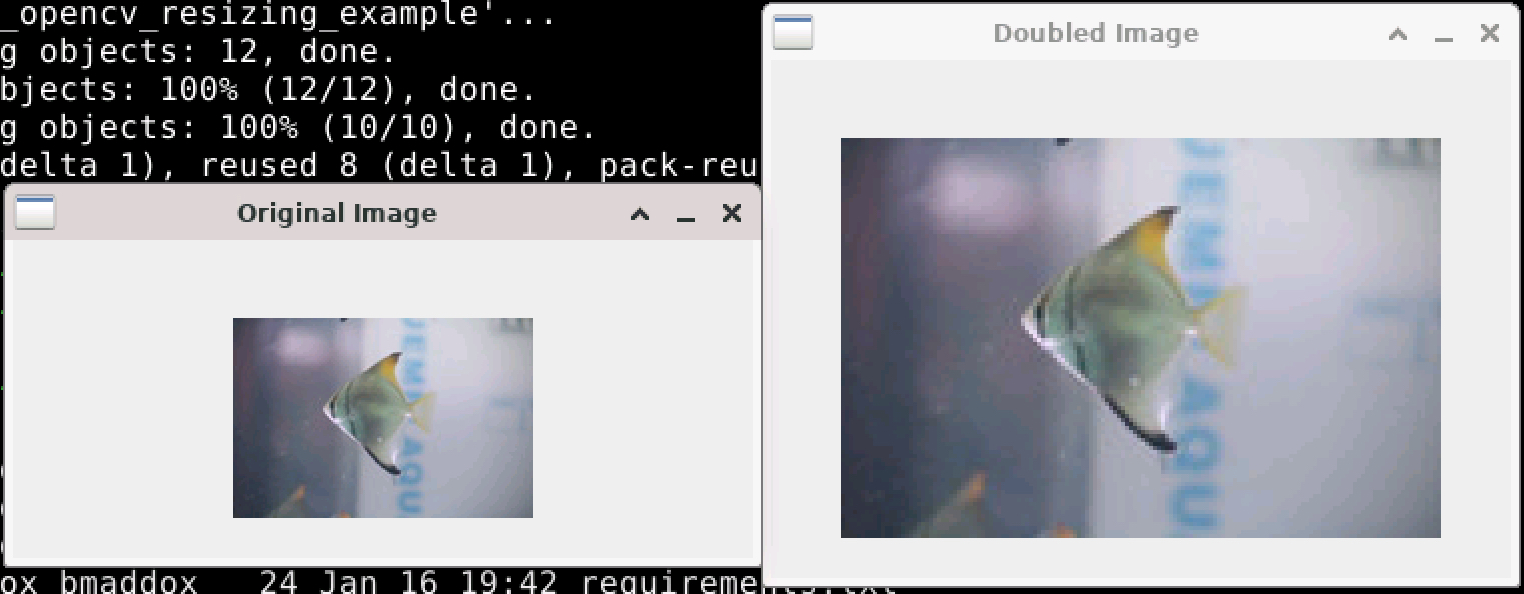
When we run this code, we see our small fish image in a window:
Next we will do a “dumb” resize of the image. Here we double each pixel in the X- and Y-directions. This has the effect of making the image 2x large, effectively zooming in to the image.
empty_mat = numpy.zeros((height * 2, width * 2, channels), dtype=numpy.uint8)
Here empty_mat is an empty image that has been initialized to all zeroes. Numpy is a well known array library that OpenCV and other packages are built on. When OpenCV and Python load an image, they store it in what is basically a three dimensional array. You can think of this as a box where each red, green, and blue channel of the image is contained in the box.
We do the following loop now to copy the pixel to the output empty_mat:
for y in range(height):
for x in range(width):
pixel = input_image[y, x]
empty_mat[y * 2, x * 2] = pixel
empty_mat[y * 2, x * 2 + 1] = pixel
empty_mat[y * 2 + 1, x * 2] = pixel
empty_mat[y * 2 + 1, x * 2 + 1] = pixel
I used a simple loop and assignments to make it easier to see what I am doing. This loop simply goes through each row of the input image and copies that pixel to four pixels in the output image, effectively doubling the size and zooming the image.
Now we display both the original image and the doubled one.
cv2.imshow("Original Image", input_image)
cv2.imshow("Doubled image", empty_mat)
cv2.waitKey(0)
cv2.destroyAllWindows()
In the above screenshot, we can see that the image has indeed been “zoomed” in and is now twice the size of the original. Semantically, both images are equal to each other. You can see the jaggedness of the fish in the doubled image due to the simplistic nature of the resize. The main take away from this is that it is still the same image, even if it is larger than the original.
Most applications that let you zoom in or resize images use something a bit smarter than a simple doubling of each pixel. As you can see with the above images, the simple “doubling” results in a jagged image that becomes less visually pleasing as the zoom multiplier gets larger. This is because to double an image using the simple method, each pixel becomes four pixels. Four times larger means eight pixels, and so on. This method also becomes much more complicated if the zoom factor is not an even multiple of two.
Images today are resized using mathematical interpolations. Wikipedia defines interpolation as “a type of estimation, a method of constructing (finding) new data new points based on the range of a discrete set of known data points.” “Ah ha!” you might say, this sounds like things are being made up. And yes they are, but data is not being made up out of the blue. Instead, interpolations use existing data to mathematically predict data to fill in the gaps. Google, Apple, and other mapping applications use interpolations to fill in the gaps of your position to display on the screen in-between calculating your exact position using the satellites. Our brains do it when we reach out to catch a fast ball. Weather and financial forecasters use it every day.
Interpolations have a long history in mathematics. The Babylonians were using linear and other interpolations as far back as the 300’s BCE to predict the motions of celestial bodies. As time has gone on, mathematicians have devised better and more accurate methods of predicting values based on existing ones. Over time, we have gone from the relatively simplistic piecewise constant interpolations to Gaussian processes. Each advance has made better and closer predictions to what the missing values actually are.
Consider an example using linear interpolation. This type of problem is often taught in geometry and other math classes. Assume that we have points on a two-dimensional XY axis such as below.
Here we see we are given a series of (1,1), (3,3), (4,4), (5,5), (6,6), and (7,7). This is in fact a plot of the function y = x, except I omitted the point (2,2). We can eyeball and see that the missing y value for x=2 is in fact 2, but let us go through the math.
The formula for linear interpolation is: ![]() . So if we want to solve for the point where x=2, (x1,y1) will be the point (1,1) and (x2, y2) will be the point (3,3). Plugging these numbers in we get
. So if we want to solve for the point where x=2, (x1,y1) will be the point (1,1) and (x2, y2) will be the point (3,3). Plugging these numbers in we get ![]() , which indeed gives us y=2 for x=2. No magic here, just math.
, which indeed gives us y=2 for x=2. No magic here, just math.
Other types of interpolations, such as cubic, spline, and so on, also have mathematical equations that calculate new values based on existing values. This point is important to note. All interpolations use math to calculate new values based on existing ones. These interpolations have been used over hundreds of years, and are the basis for many things we use today. No magic, no guessing, no making things up. I think we can trust them.
So let us get back to image processing. OpenCV fortunately can use interpolation to resize an image. As a reminder, we typically do this so that the image is more pleasing to the eye. Interpolations give us images that are not blocky as in the case of the simple image doubling technique. First we will use linear interpolation to double the size of the image
double_width = width * 2
double_height = height * 2
linear_double_image = cv2.resize(input_image, (double_width, double_height), interpolation=cv2.INTER_LINEAR)
# Now display both the original and the linear interpolated image to compare.
cv2.imshow("Original Image", input_image)
cv2.imshow("Linear Interpolated image", linear_double_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
To make things explicit, we set new dimensions to twice the width and height of the image and use linear interpolation to scale the image up.
Here we see that the interpolated image is not as blocky as the simple pixel doubling image, meaning that yes the new image is a bit different from the original. However, nothing new has been added to the image. It has not been distorted and the same semantic content has been preserved. We can look at what has happened by examining the coordinates at pixel (0,0) in the original image.
Let us take this farther now. What happens if we increase to four times the original size?
# Linear interpolation to quad size
quad_width = width * 4
quad_height = height * 4
linear_quad_image = cv2.resize(input_image, (quad_width, quad_height), interpolation=cv2.INTER_LINEAR)
# Now display both the original and the linear interpolated image to compare.
cv2.imshow("Original Image", input_image)
cv2.imshow("Linear Interpolated 4x image", linear_quad_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
Again, creating a 4x-size image does not introduce any new objects or change the semantic meaning of the image. You may notice that it looks a bit more blurry than the 2x image. This is because linear interpolation is a simple process.
Let us see what it looks like using a more rigorous cubic interpolation to create a 4x image.
# Cubic interpolation
cubic_quad_image = cv2.resize(input_image, (quad_width, quad_height), interpolation=cv2.INTER_CUBIC)
# Now display both the original and the linear interpolated image to compare.
cv2.imshow("Original Image", input_image)
cv2.imshow("Cubic Interpolated 4x image", cubic_quad_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
We can see that the image does not have as pronounced blockiness that the linearly interpolated image has. Yes, it is not exactly the same as the original image as we did not simply double each pixel. However, the semantic contents of the image are the same, even using a different interpolation method. We did not introduce anything new into the image by resizing it. The meaning of the image is the same as it was before. It is just larger so we can see it better.
It is time to wrap this up as it is a longer post than I intended. You can see from the above that resizing (or zooming in on) an image does not change the content of the image. We did not turn the fish into a shark by enlarging it. We did not add another fish to the image by enlarging it.
I encourage you to try this on your own at home. Pull out your phone, take a picture, and then zoom in on it. Your camera likely takes such a high resolution that displaying it on your screen actually reduces some detail, so that you have to zoom in to see the fine detail in the image. Ask yourself though, is the meaning of the image changed by zooming in or out on it? Are they still your children, or did zooming in turn them into something else?
I hope that the next time you hear something in the news about image processing, you realize that every algorithm that does this is just math. It is either math to bring out fine details that you cannot normally see in the case of dark images, or math that makes the image larger so that you can better see the smile on a child. The content of the image is not changed, it is always semantically the same as the original image.